[LeetCode] 29. Divide Two Integers

---

카테고리 : Dynamic Programming
난이도 : Medium

---

Longest String Chain - LeetCode

아이디어

문제에서는 words라는 문자열의 배열이 주어진다.

• predecessor : 문자열 word1에서 문자들의 순서를 바꾸지 않고 하나의 문자를 아무데나 추가로 삽입했을 때 word2를 만들 수 있다면 word1을 word2의 predecessor라 한다.
• word chain : words 배열에서 한 개 이상의 문자열을 선택해서 [word1, word2, word3, ... , wordk]라는 배열을 만들었을 때 word1은 word2의 predecessor이고 word2는 word3의 predecessor이고, ... wordk-1은 wordk의 predecessor일 때 이 시퀀스를 word chain이라 한다.

구해야 하는 것은 words에서 구할 수 있는 가장 긴 word chain의 길이다.

가장 긴 증가하는 부분 수열

문제를 보고 생각났던 문제는 가장 긴 증가하는 부분 수열 찾기였다. 이 문제와 가장 긴 증가하는 부분 수열 문제와 매우 비슷하다고 느꼈는데, 가장 긴 증가하는 부분 수열 문제는 아래와 같다.

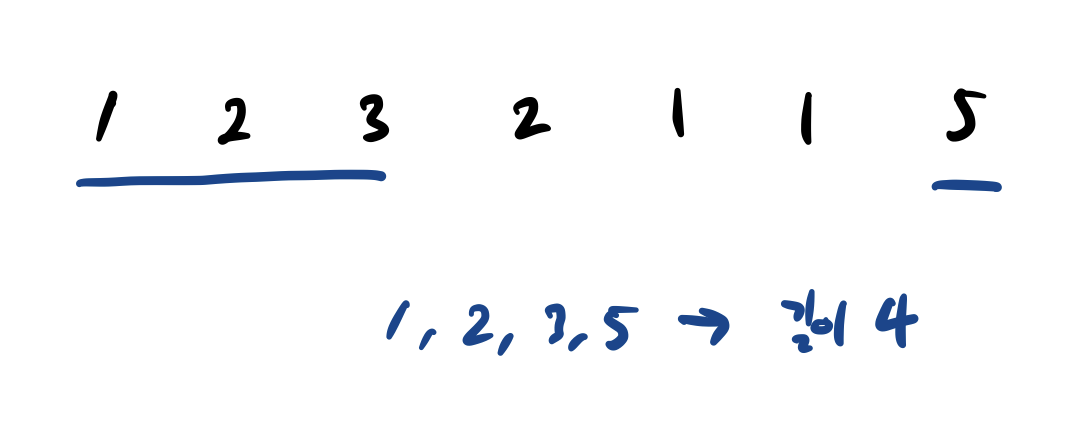
수들의 배열이 있을 때 이 부분 수열 중 오름차순이면서 길이가 가장 긴 부분 수열을 구하는 문제다. 이 문제를 구할 때는 다이나믹 프로그래밍으로 문제를 풀었다. 이전에 구한 작은 문제에서 큰 문제의 답을 구하는 방법인데, 그 방법은 아래와 같다.

D[i] 를 i번째 원소로 끝나는 가장 긴 증가하는 부분 수열의 길이라고 해보자. i번째 원소로 끝난다는 것은 i번째 원소를 포함한다는 뜻으로, 기본값은 1이 될 것이다.(i번째 원소만 부분 수열로 존재할 때 길이는 1이다.)

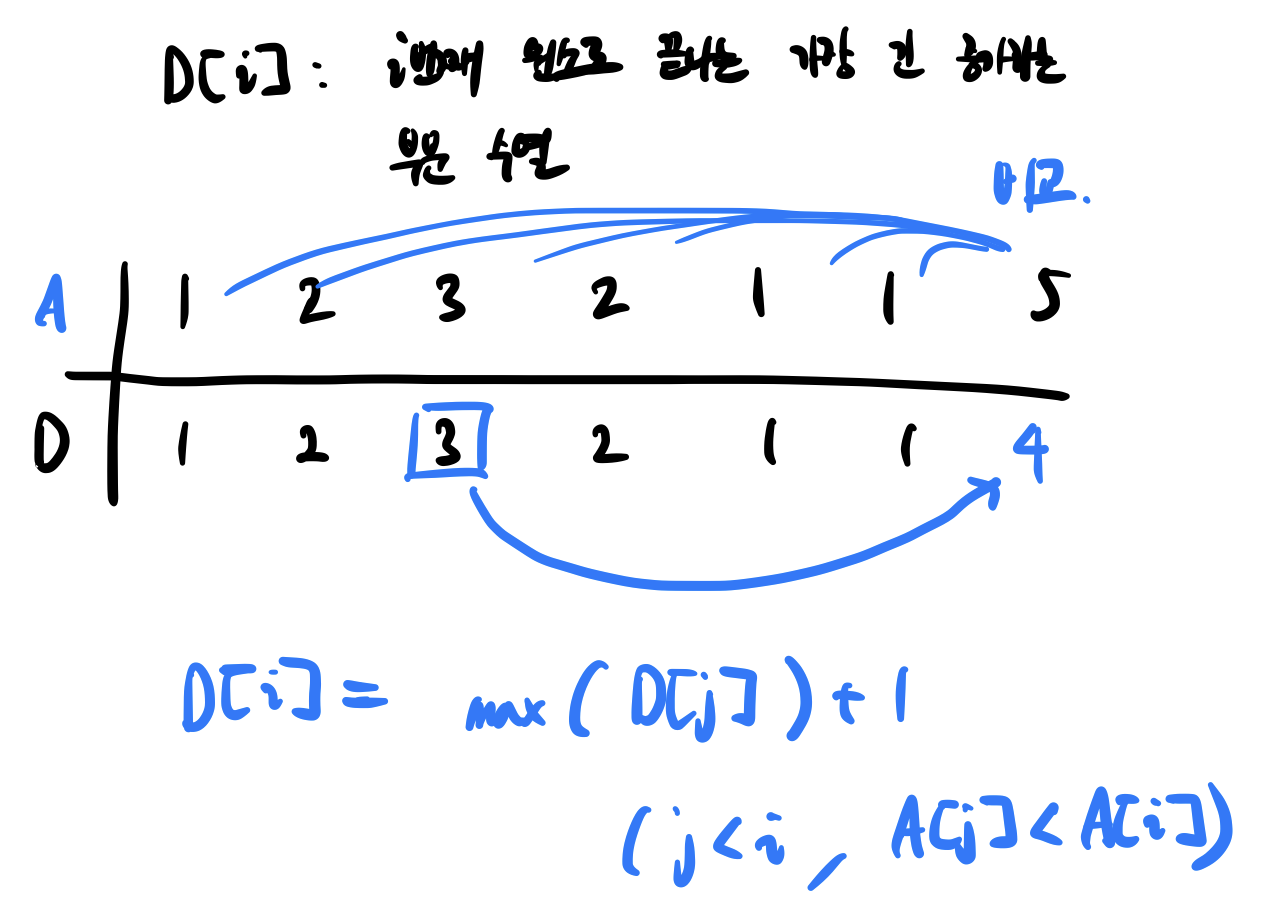
• D[1] : 1번째 원소 전에는 원소가 없으므로 D[1] = 1
• D[2] : 2번째 원소 전의 1번째 원소와 2번째 원소를 비교. 2번째 원소가 더 크기 때문에 1번째 원소는 2번째 원소 앞에 올 수 있다. 따라서 D[2] = D[1] + 1 = 2
• D[3] : 3번째 원소 전의 2번째 원소와 비교. 2번째 원소 < 3번째 원소 이므로 2번째 원소는 3번째 원소 앞에 올 수 있다. 따라서 D[3] = D[2] + 1 = 3으로 업데이트 할 수 있다. 1번째 원소와도 비교해서 D[3] = D[1] + 1로 업데이트 할 수 있지만 이미 3이라는 max 값이 존재하기 때문에 D[3] = 3이 된다.
• ...

이를 통해 점화식을 세울 수 있다.

 

D[i] = max(D[j]) + 1 ( j < i, A[j] < A[i] )

응용

이 방법을 사용해서 Longest String Chain 문제도 해결할 수 있을 것으로 보인다.

가장 긴 증가하는 부분 수열을 구하는 문제와 다른 점을 D[i]를 구할 때 A[j]가 A[i]의 predecessor일 경우에만 D[i]를 업데이트 해주는 부분밖에 없다.

 

다만 여기에서 유의해야 할 점은 D[i]를 설정할 때 앞의 원소들과 비교하는데, 만약 i번째 원소 뒤에 i번째 원소의 predecessor가 될 수 있는 원소가 있으면 안된다. 따라서 words를 먼저 길이 순으로 정렬해서 쉽게 비교할 수도 있다.

코드

class Solution:
    def longestStrChain(self, words: List[str]) -> int:
        # O(nlogn), 길이 순으로 words 정렬
        words.sort(key = lambda x: len(x))

        # D[i]의 기본값은 1이다.
        D = [1] * len(words)

        # wordA가 wordB의 predecessor인지 확인하는 함수
        # O(len(wordB))
        def isPredecessor(wordA, wordB):
            # 길이 차이가 꼭 1이 나야 한다.
            if len(wordA) + 1 != len(wordB):
                return False

            # 다른 문자의 개수
            diffCount = 0
            # wordA, wordB 각각의 포인터
            p1, p2 = 0, 0

            # wordA, wordB 범위 내에서 비교
            while p1 < len(wordA) and p2 < len(wordB):
                # 문자가 다르면
                if wordA[p1] != wordB[p2]:
                    # 다른 문자의 개수를 증가시키고 wordB의 다음 문자로 넘어간다.
                    diffCount += 1
                    p2 += 1
                # 문자가 같으면 wordA, wordB의 다음 문자로 넘어간다
                else:
                    p1 += 1
                    p2 += 1

                # 문자가 하나 이상 다르면 거짓
                if diffCount > 1:
                    return False

            if diffCount > 1:
                return False

            return True

        # O(1000^2) * 16
        # 문제의 개수 len(words)개 = 1000
        # 문제 하나를 푸는데 앞선 모든 원소 len(words) 개에 대해 isPredecessor 함수 실행 = len(words) * len(max(wordB)) = 16 * 1000
        for i in range(1, len(words)):
            for j in range(0, i):
                # words[j]가 words[i]의 predecessor일 때 업데이트
                if isPredecessor(words[j], words[i]):
                    D[i] = max(D[i], D[j] + 1)

        return max(D)

결과를 보니 시간이 오래 걸리는 편이었던 것 같다. 따라서 시간을 줄일 수 있는 부분을 생각하보니 아래와 같이 정리할 수 있었다.

• 정말 words를 정렬할 필요가 있는가? => DP로 답을 구하기 위해서는 작은 크기의 문제를 먼저 풀어야 하므로 꼭 정렬은 필요하다.
• isPredecessor의 시간 복잡도를 줄일 수 있는가? => 앞의 문자열이 predecessor인지 비교하는 대신에 단어 자체의 predecessor로 만들어 해당 predecessor가 words배열에 존재하는 지를 확인하면 어떨까

class Solution:
    def longestStrChain(self, words: List[str]) -> int:
        words.sort(key=lambda x: len(x))

        # 이미 등장한 단어들(탐색한 단어들을 담는 딕셔너리). 단어 : 단어로 끝나는 가장 긴 word chain의 길이. 위 해답의 D 배열과 같은 역할을 한다.
        existingWords = dict()
        ans = 0

        # O(len(words)) = 1000
        for word in words:
            maxLength = 1
            # word마다 word의 predecessor를 만들어버린다.
            # O(len(word)) = 16
            for i in range(0, len(word)):
                # O(len(word)) = 16. 문자열 slicing 시간 복잡도는 슬라이싱 하는 문자열 길이가 k일 경우 O(k)라 한다.
                predecessorCandidate = word[:i] + word[i+1:]
                # `words` 배열에 predecessor가 있는 경우
                # O(1)
                if predecessorCandidate in existingWords:
                    maxLength = max(existingWords[predecessorCandidate] + 1, maxLength)
            existingWords[word] = maxLength
            ans = max(ans, maxLength)

        return ans

훨씬 빨라지긴 했다. 전체 문제의 시간복잡도를 계산하면 (16^2) * 1000 정도로 개선되어 더 빨라진 것으로 보인다.